https://www.acmicpc.net/problem/16884
16884번: 나이트 게임
첫째 줄에 테스트 케이스의 개수 T(1 ≤ T ≤ 100)가 주어진다. 둘째 줄부터 T개의 줄에 테스트 케이스가 한 줄에 하나씩 주어지며, 체스판의 크기 N(1 ≤ N ≤ 10,000)으로 이루어져 있다.
www.acmicpc.net
<문제>
나이트 게임은 크기가 N×N인 체스판 위에서 진행되는 게임이고, 나이트를 하나씩 턴을 번갈아가며 놓는 게임이다.
나이트는 이미 놓여 있는 나이트가 공격할 수 있는 칸에 놓을 수 없다. 나이트를 (r, c)에 놓은 경우에는 (r-2, c+1), (r-1, c+2), (r+1, c+2), (r+2, c+1), (r+2, c-1), (r+1, c-2), (r-1, c-2), (r-2, c-1)이 공격할 수 있는 칸이다.
나이트를 놓을 수 있는 칸이 없는 사람이 게임을 지게 된다. 구사과와 큐브 러버가 이 게임을 최적의 방법으로 플레이했을 때, 이기는 사람을 구하는 프로그램을 작성하시오. 게임은 구사과가 먼저 시작한다.
<입력>
첫째 줄에 테스트 케이스의 개수 T(1 ≤ T ≤ 100)가 주어진다. 둘째 줄부터 T개의 줄에 테스트 케이스가 한 줄에 하나씩 주어지며, 체스판의 크기 N(1 ≤ N ≤ 10,000)으로 이루어져 있다.
<출력>
각각의 테스트 케이스마다 게임을 이기는 사람을 출력한다. 구사과가 이기는 경우에는 "koosaga", 큐브 러버가 이기는 경우에는 "cubelover"를 출력한다.
<풀이>
먼저 문제의 입력제한이 1초였기 때문에 Brute Force 방향이 아닌, Game 문제에 대한 풀이로 접근했다.
일정한 규칙이 존재하고, 그 규칙을 통해 답을 유추하는 문제로 생각했다.
n=1일 때는 자명하게 첫 번째 플레이어가, n=2일 때는, 2번째 플레이어가 승리한다.
먼저 기본적인 풀이인 DP로 접근했지만, N보다 작은 N-1 혹은 N-2에 대한 결과로 N에 대한 최적의 방법
유추할 수 있을까? 라고 고민했지만 큰 관련성을 찾기는 힘들었다.
승자를 구하기 위해서 굳이 프로그래머가 최적의 방법을 알아야 할까?라는 의문을 가졌고, 일단 N=3까지의 경우까지는 손으로 그려 보았다.
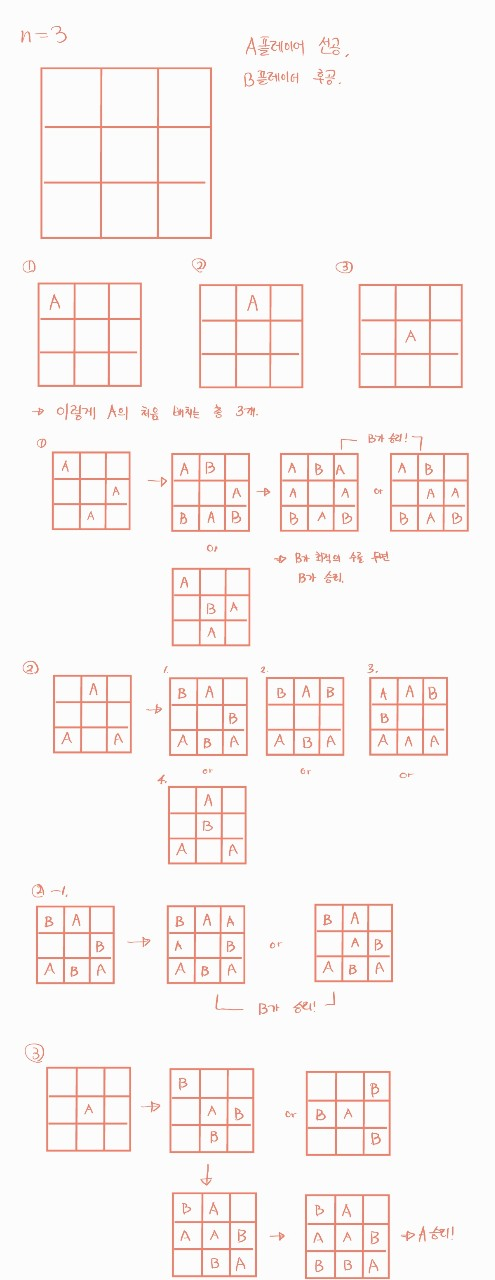
보다시피 N=3인 경우, 선공 플레이어가 가운데 두는 경우, 최적의 방법으로 승리할 수 있다.
여기서부터 뭔가 홀수인 경우, 선공이 승, 짝수인 경우, 후공이 승이 아닐까?라는 의심과 함께 접근했다.
생각을 오래오래 하다가 결국 답은 맞았지만, 증명을 하지 못해서 검색했는데
https://steady-coding.tistory.com/212
[BOJ] 백준 16884번 : 나이트 게임 (JAVA)
문제 나이트 게임은 크기가 N×N인 체스판 위에서 진행되는 게임이고, 나이트를 하나씩 턴을 번갈아가며 놓는 게임이다. 나이트는 이미 놓여져 있는 나이트가 공격할 수 있는 칸에 놓을 수 없다.
steady-coding.tistory.com
위 링크를 보고 아이디어를 얻었다.
선공, 후공 나눠진 상황에서 최선의 방법은 무엇일까? N에 따라 승,패가 결정된다는 게 무슨 뜻을 가질까?
게임 문제 접근 강의에서 배운,
선공 입장에서 만약 내가 지는 형태의 상황이라면, 가능하면 의미없는 수를 두어서 본인이 후공 입장이 되어 승리하는 케이스가 아닐까?라는 접근 방식이 들었다.
위의 블로그 링크를 요약하자면, 후공 입장에서는 선공의 수를 체스판의 원점에 대해 점대칭을 하여, 따라 두면 된다. 그러면 점 대칭으로 기준으로 항상 같고, 체스판에서 둘 수 없는 곳은 항상 짝수가 된다.
후공은 점대칭을 통해 두면 최적의 수이지만, 선공 입장에서도, 점대칭을 찾을 수 없는
N이 홀수인 경우, 원점에 첫 수를 두면, 의미 없는 수가 되어 선공이 사실상 후공이 된다.
이후에는, 마찬가지로 선공이 후공의 수를 점대칭으로 따라 두면 된다.

<코드>
#include <iostream>
using namespace std;
using ll = long long;
int main(void) {
ios_base::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
int n, t;
cin >> t;
for (int i = 0; i < t; i++) {
cin >> n;
// n*n 크기의 체스판에 나이트를 배치할 수 있으며,
// 각 플레이어는 나이트의 공격을 받지 않는 곳에만 새로운 나이트를 배치 가능하다.
// 더 이상 배치할 수 없는 플레이어가 패배
// 선공이 어딜 놓든 가운데 점을 원점으로 해서 점대칭을 취해 반대 위치에 놓으면 된다
// 그러면, 선공이 놓은 나이트가 공격 가능한 위치의 점대칭이 후공의 점대칭이고,
// 이렇게 턴이 진행되다보면, 후공이 끝나고 나면, 남은 위치는 매번 짝수
// -> 점대칭 기준으로 완전한 대칭이기 때문에
// N이 짝수면 항상 선공이 패배하지만,
// N이 홀수이면, 선공이 가운데 원점에 해당하는 부분에 첫 수를 두게 되면,
// 후공이 선공이 되는 것과 같은 효과를 내기 때문에, 선공이 승리한다.
if (n % 2 == 1) cout << "koosaga" << "\n";
else cout << "cubelover" << "\n";
}
return 0;
}'Problem Solving > 백준 1일 1커밋' 카테고리의 다른 글
| 백준 15877 Apples and Bannas - C++ (0) | 2022.01.23 |
|---|---|
| 백준 17965 Absolute Game - C++ (0) | 2022.01.22 |
| 백준 11049 행렬 곱셈 순서 - C++ (0) | 2022.01.20 |
| 백준 9251 LCS - C++ (0) | 2022.01.20 |
| 백준 9177 가장 큰 증가 부분 수열 - C++ (0) | 2022.01.20 |